Mã hóa Huffman là gì?
|
|
Bài viết này cần thêm chú thích nguồn gốc để kiểm chứng thông tin.
|
Trong khoa học máy tính và lý thuyết thông tin, mã hóa Huffman là một thuật toán mã hóa dùng để nén dữ liệu. Nó dựa trên bảng tần suất xuất hiện các ký tự cần mã hóa để xây dựng một bộ mã nhị phân cho các ký tự đó sao cho dung lượng (số bit) sau khi mã hóa là nhỏ nhất.
Tác giả
Thuật toán được đề xuất bởi David A. Huffman khi ông còn là sinh viên Ph.D. tại MIT, và công bố năm 1952 trong bài báo “A Method for the Construction of Minimum-Redundancy Codes”. Sau này Huffman đã trở thành một giảng viên ở MIT và sau đó ở khoa Khoa học máy tính của Đại học California, Santa Cruz, Trường Kỹ nghệ Baskin (Baskin School of Engineering).
Dẫn nhập
Mã tiền tố
Để mã hóa các ký hiệu (ký tự, chữ số,…) ta thay chúng bằng các xâu nhị phân, được gọi là từ mã của ký hiệu đó.
Chẳng hạn bộ mã ASCII, mã hóa cho 256 ký hiệu là biểu diễn nhị phân của các số từ 0 đến 255, mỗi từ mã gồm 8 bit. Trong ASCII từ mã của ký tự “a” là 1100001, của ký tự “A” là 1000001. Trong cách mã hóa này các từ mã của tất cả 256 ký hiệu có độ dài bằng nhau (mỗi từ mã 8 bit). Nó được gọi là mã hóa với độ dài không đổi.
Khi mã hóa một tài liệu có thể không sử dụng đến tất cả 256 ký hiệu. Hơn nữa trong tài liệu chữ cái “a” chỉ có thể xuất hiện 1000000 lần còn chữ cái “A” có thể chỉ xuất hiện 2, 3 lần. Như vậy ta có thể không cần dùng đủ 8 bit để mã hóa cho một ký hiệu, hơn nữa độ dài (số bít) dành cho mỗi ký hiệu có thể khác nhau, ký hiệu nào xuất hiện nhiều lần thì nên dùng số bit ít, ký hiệu nào xuất hiện ít thì có thể mã hóa bằng từ mã dài hơn. Như vậy ta có việc mã hóa với độ dài thay đổi. Tuy nhiên, nếu mã hóa với độ dài thay đổi, khi giải mã ta làm thế nào phân biệt được xâu bít nào là mã hóa của ký hiệu nào. Một trong các giải pháp là dùng các dấu phẩy (“,”) hoặc một ký hiệu quy ước nào đó để tách từ mã của các ký tự đứng cạnh nhau. Nhưng như thế số các dấu phẩy sẽ chiếm một không gian đáng kể trong bảng mã. Một cách giải quyết khác dẫn đến khái niệm mã tiền tố
- Mã tiền tố là bộ các từ mã của một tập hợp các ký hiệu sao cho từ mã của mỗi ký hiệu không là tiền tố (phần đầu) của từ mã một ký hiệu khác trong bộ mã ấy.
Đương nhiên mã hóa với độ dài không đổi là mã tiền tố.
- Ví dụ: Giả sử mã hóa từ “ARRAY”, tập các ký hiệu cần mã hóa gồm 3 chữ cái “A”,”R”,”Y”.
- Nếu mã hóa bằng các từ mã có độ dài bằng nhau ta dùng ít nhất 2 bit cho một chữ cái chẳng hạn “A”=00, “R”=01, “Y”=10. Khi đó mã hóa của cả từ là 0001010010. Để giải mã ta đọc hai bit một và đối chiếu với bảng mã.
- Nếu mã hóa “A”=0, “R”=01, “Y”=11 thì bộ từ mã này không là mã tiền tố vì từ mã của “A” là tiền tố của từ mã của “R”. Để mã hóa cả từ ARRAY phải đặt dấu ngăn cách vào giữa các từ mã 0,01,01,0,11
- Nếu mã hóa “A”=0, “R”=10, “Y”=11 thì bộ mã này là mã tiền tố. Với bộ mã tiền tố này khi mã hóa xâu “ARRAY” ta có 01010011.
Biểu diễn mã tiền tố trên cây nhị phân
- Nếu có một cây nhị phân
n
{displaystyle n}
lá ta có thể tạo một bộ mã tiền tố cho
n
{displaystyle n}
ký hiệu bằng cách đặt mỗi ký hiệu vào một lá. Từ mã của mỗi ký hiệu được tạo ra khi đi từ gốc tới lá chứa ký hiệu đó, nếu đi qua cạnh trái thì ta thêm số 0, đi qua cạnh phải thì thêm số 1.
- Ví dụ: Cây 3 lá sau đây biểu diễn bộ mã của A,R,Y trong ví dụ trên
* 0/ 1 A * 0/ 1 R Y
- Từ mã của “A” là 0, của “R” là 10, của “Y” là 11.
Mã tiền tố tối ưu
Từ ví dụ trên thấy mã hóa của xâu “ARRAY” bằng mã độ dài cố định mất 10 bit, bằng mã tiền tố đã đưa ra mất 8 bit, tiết kiệm được 20%. Bài toán đặt ra là bộ mã tiền tố đã tối ưu chưa.
Bài toán
- Cho tập A các ký hiệu và trọng số (tần suất) của chúng.
- Tìm một bộ mã tiền tố với tổng độ dài mã hóa là nhỏ nhất.
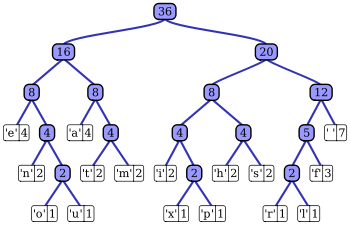
Cây Huffman sinh ra từ xâu ký tự “this is an example of a huffman tree”. Tổng số bit để mã hóa là 135, không kể các ký tự trống.
Dữ liệu
- Input
Bảng
n
{displaystyle n}
chữ cái
A
=
{
a
1
,
a
2
,
⋯
,
a
n
}
{displaystyle A=left{a_{1},a_{2},cdots ,a_{n}right}}
.
Tập các trọng số (tần suất xuất hiện) tương ứng
W
=
{
w
1
,
w
2
,
⋯
,
w
n
}
{displaystyle W=left{w_{1},w_{2},cdots ,w_{n}right}}
, ví dụ:
w
i
=
w
e
i
g
h
t
(
a
i
)
,
1
≤
i
≤
n
{displaystyle w_{i}=mathrm {weight} left(a_{i}right),1leq ileq n}
.
- Output
Bộ mã
C
(
A
,
W
)
=
{
c
1
,
c
2
,
⋯
,
c
n
}
{displaystyle Cleft(A,Wright)=left{c_{1},c_{2},cdots ,c_{n}right}}
, là tập hợp các từ mã (nhị phân), trong đó
c
i
{displaystyle c_{i}}
là từ mã của
a
i
,
1
≤
i
≤
n
{displaystyle a_{i},1leq ileq n}
.
- Yêu cầu
Đặt
L
(
C
)
=
∑
i
=
1
n
w
i
×
l
e
n
g
t
h
(
c
i
)
{displaystyle Lleft(Cright)=sum _{i=1}^{n}{w_{i}times mathrm {length} left(c_{i}right)}}
là trọng số của bộ mã
C
{displaystyle C}
. Điều kiện là:
L
(
C
)
≤
L
(
T
)
{displaystyle Lleft(Cright)leq Lleft(Tright)}
với mọi bộ mã
T
(
A
,
W
)
{displaystyle Tleft(A,Wright)}
.
Ví dụ
- Trong ví dụ sau, với các tần số như trên mã 1 sẽ tốn không gian hơn mã 2.
| Input | Ký tự | a | b | c | d | e | |
|---|---|---|---|---|---|---|---|
| tần suất | 0.10 | 0.15 | 0.30 | 0.16 | 0.29 | 1,00 | |
| Mã 1 | Từ mã | 000 |
001 |
010 |
011 |
110 |
|
| Độ dài từ mã (bits) | 3 | 3 | 3 | 3 | 3 | 3,00 | |
| Mã 2 | Từ mã | 000 |
001 |
10 |
01 |
11 |
|
| Độ dài từ mã (bits) | 3 | 3 | 2 | 2 | 2 | 2,25 |
Giải thuật
Giải thuật tham lam
Trong giải thuật tham lam giải bài toán xây dựng cây mã tiền tố tối ưu của Huffman, ở mỗi bước ta chọn hai chữ cái có tần số thấp nhất để mã hóa bằng từ mã dài nhất.
Giả sử có tập A gồm
n
{displaystyle n}
ký hiệu và hàm trọng số tương ứng
W
(
i
)
,
i
=
1..
n
{displaystyle W(i),i=1..n}
.
- Khởi tạo: Tạo một rừng gồm n cây, mỗi cây chỉ có một nút gốc, mỗi nút gốc tương ứng với một ký tự và có trọng số là tần số/tần suất của ký tự đó
W
(
i
){displaystyle W(i)}
.
- Lặp:
- Mỗi bước sau thực hiện cho đến khi rừng chỉ còn một cây:
- Chọn hai cây có trọng số ở gốc nhỏ nhất hợp thành một cây bằng cách thêm một gốc mới nối với hai gốc đã chọn. Trọng số của gốc mới bằng tổng trọng số của hai gốc tạo thành nó.
Như vậy ở mỗi bước số cây bớt đi một. Khi rừng chỉ còn một cây thì cây đó biểu diễn mã tiền tố tối ưu với các ký tự đặt ở các lá tương ứng.
Ví dụ
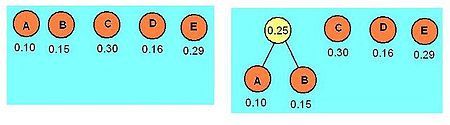
Cho bảng tần suất của 5 chữ cái A, B, C, D, E như sau tương ứng là 0.10; 0.15; 0.30; 0.16; 0.29
| A | B | C | D | E |
| 0.10 | 0.15 | 0.30 | 0.16 | 0.29 |
Quá trình xây dựng cây Huffman diễn ra như sau:
 |
|
 |
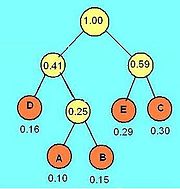 |
Như vậy bộ mã tối ưu tương ứng là:
| A | B | C | D | E |
| 010 | 011 | 11 | 00 | 10 |
Hàng đợi có ưu tiên
Trong mỗi bước của thuật toán xây dựng cây Huffman, ta luôn phải chọn ra hai gốc có trọng số nhỏ nhất. Để làm việc này ta sắp xếp các gốc vào một hàng đợi ưu tiên theo tiêu chuẩn trọng số nhỏ nhất. Một trong các cấu trúc dữ liệu thuận lợi cho tiêu chuẩn này là cấu trúc đống (với phần tử có trọng số nhỏ nhất nằm trên đỉnh của đống).
Mã giả
Trong đoạn mã giả dưới đây ta dựa trên một mảng các ký hiệu
A
[
1..
n
]
{displaystyle A[1..n]}
có tần suất tương ứng là
W
[
1..
n
]
{displaystyle W[1..n]}
Tạo hàng đợi bằng đống (heap)
Ta tạo một đống trên cơ sở sắp xếp lại các chỉ số của A và W. Ta lưu trữ đống dưới dạng mảng, ký hiệu nó là Heap[1..n]. Trước hết đưa chỉ số của các chữ cái theo thứ tự ban đầu vào mảng Heap[1..n] với Heap[i]=i. với mọi i=1..n.
Procedure DownHeap(List W,Int k,Int Count)
{
Int i:=k, v:=W(Heap(k)), j
While 2*i<=Count {
j:=2*i
if j+1<= Count and W(Heap(j+1))>W(Heap(j)) then j:=j+1
if W(Heap(j))< v then Heap(i):=Heap(j)
else break
i:=j
Heap(j):=Heap(k)
}
}
Procedure MakeHeap(List W,Int n)
{
Int k
For k:=int(n/2) downto 1 {
DownHeap (W,k,n)
}
}
Xây dựng cây Huffman
Ta sẽ lưu trữ cấu trúc của cây mã Huffman vào một mảng. Cây Huffman gồm n lá mỗi lá chứa chỉ số của chữ cái tương ứng. Mỗi lần ghép 2 cây thành một ta phải thêm một đỉnh, như vậy cây biểu diễn mã Huffman gồm 2.n-1 đỉnh. Ta ký hiệu cây này là Huff[1..2n-1]. Vì mỗi gốc mới bổ sung đều có trọng số nên ta mở rộng mảng W[1..n] các trọng số thành mảng W’ [1..2n-1]. Gọi m là số đỉnh của cây sẽ xây dựng. lúc đầu ta có n lá, đỉnh bổ sung lần đầu sẽ là n+1, lần thứ 2 là n+2,… Khi lấy ra hai ký tự có tần số nhỏ nhất chẳng hạn ký tự thứ i làm con trái và ký tự thứ j làm con phải của đỉnh mới bổ sung có chỉ số m ta đặt Huff[i]=-m, Huff[j]=m.
Procedure MakeTreeHuffman(List W,Int n)
{
List Heap,Huff
Int i,j,count:=n,m:=n
MakeHeap(W,n)
While Count >1 {
i:=Heap(1)
Heap(1):= Heap(count)
Count:=Count-1
DownHeap(W,1,Count)
j:=Heap(1)
m:=m+1
Huff(i):=-m
Huff(j):=m
W(m):=W(i)+W(j)
Heap(1):=m
DownHeap(W,1,Count)
}
Return Huff
}
Xây dựng bộ mã
Sau khi cấu trúc của cây Huffman được lưu vào mảng Huff ta dễ dàng xây dựng mảng Code[1..n] cho bộ mã nhị phân tiền tố tối ưu của các ký tự A[1..n].
Procedure CodingHuffman(List Huff, n){
Int k:=1,j
While k<=n {
Code(k):=""
j:=Huff(k)
While Abs(j)<=2*n-1 {
If j>0 then Code(k)="1"+Code(k)
else Code(k)="0"+Code(k)
j:=Huff(abs(j))
}
k:=k+1
}
Return Code
}
Nén file bằng mã Huffman
Trong các bước trên, giả sử đã xây dựng được bộ mã Huffman của 256 ký hiệu có mã ASCII từ 0 đến 255 chứa trong mảng Code[1..256].
Việc nén file có thể phân tích sơ bộ như sau:
- Đọc từng byte của file cần nén cho đến khi hết tệp,
- Chuyển theo bộ mã thành xâu nhị phân,
- Ghép với xâu nhị phân còn dư từ bước trước,
- Nếu có đủ 8 bit trong xâu thì cắt ra tám bít đầu tiên ghi vào tệp nén,
- Nếu đã hết tệp cần nén thì dừng…
Xem thêm
- Mã Shannon-Fano
- Nén dữ liệu
- Lempel-Ziv-Welch
Tham khảo
- Huffman’s original article: D.A. Huffman, “A Method for the Construction of Minimum-Redundancy Codes”, Proceedings of the I.R.E., sept 1952, pp 1098–1102
- Background story: Profile: David A. Huffman Lưu trữ 2007-02-20 tại Wayback Machine, Scientific American, Sept. 1991, pp. 54–58
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Section 16.3, pp. 385–392.
Liên kết ngoài
- Program for explaining the Huffman Coding procedure. Lưu trữ 2008-07-01 tại Wayback Machine
- Huffman Code Applet
- n-ary Huffman Template Algorithm Lưu trữ 2005-06-18 tại Wayback Machine
- Huffman codes’ connection with Fibonacci and Lucas numbers
- Sloane A098950 Minimizing k-ordered sequences of maximum height Huffman tree
- Computing Huffman codes on a Turing Machine Lưu trữ 2005-07-31 tại Wayback Machine
- Mordecai J. Golin, Claire Kenyon, Neal E. Young “Huffman coding with unequal letter costs” (PDF), STOC 2002: 785-791
- Huffman Coding: A CS2 Assignment a good introduction to Huffman coding
- A quick tutorial on generating a Huffman tree
- Pointers to Huffman coding visualizations Lưu trữ 2007-02-27 tại Wayback Machine
- Huffman for PHP
- Huffman in C
- Huffman in Java Lưu trữ 2008-07-05 tại Wayback Machine
| Wikimedia Commons có thêm hình ảnh và phương tiện truyền tải về Mã hóa Huffman. |
- Thuật toán nén dữ liệu
- Lý thuyết mã hóa
- Khoa học máy tính năm 1952
Từ khóa: Mã hóa Huffman, Mã hóa Huffman, Mã hóa Huffman
mã hóa huffman
mã huffman
huffman
mã hóa huffman lý thuyết thông tin
các bước mã hóa huffman
phương pháp mã hóa huffman
thuật toán huffman
bài tập mã hóa huffman có lợi giải
huffman coding là gì
huff man
hufman
mã huffman động là mã
huffma
huffman wikipedia
code mã hóa huffman c
cây huffman
mã giả là gì
thuật toán nén huffman
huffman wiki
xây dựng cây huffman
huffman.
mã hoá nguồn
mã hóa nguồn là gì
nén huffman
ví dụ về mã giả


 .
. , ví dụ:
, ví dụ: .
. , là tập hợp các từ mã (nhị phân), trong đó
, là tập hợp các từ mã (nhị phân), trong đó là từ mã của
là từ mã của .
. là trọng số của bộ mã
là trọng số của bộ mã . Điều kiện là:
. Điều kiện là: với mọi bộ mã
với mọi bộ mã .
. .
.
![{displaystyle A[1..n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/77350b7b7a24749675609a440314e0ab8aded3d5) có tần suất tương ứng là
có tần suất tương ứng là![{displaystyle W[1..n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02c751c4e0bbef720b65b113b475a6f201615924)